반응형
- 위치척도
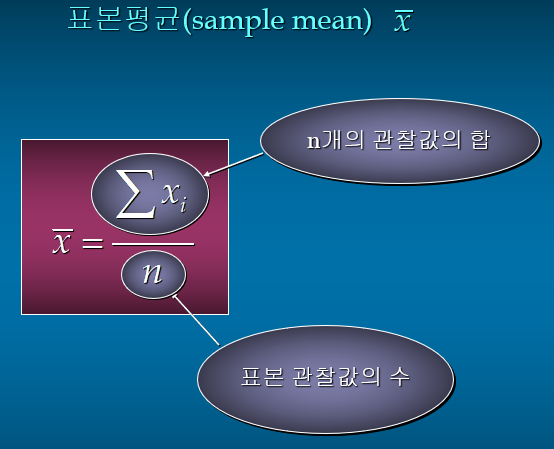
1. 평균 : 모든 자료값들의 평균
- 평균은 표본평균과 모집단 평균으로 구분할 수 있다.
참고로 모집단에서 n개를 뽑아 표본을 만들어 평균을
구한 것을 표본평균이라고 칭한다. 즉 샘플의 평균이다.

2. 중앙값
- 극단값이 포함되어 있을 때 더욱 효과적이다.
(값의 개수가 짝수인 경우 2개의 평균으로 구한다.)

3. 최빈값
- 가장 빈번하게 나타나는 값이다.
- 2개의 최빈값 = 이중모드, 3개 이상의 최빈값=다모드
-변동성 측정
1. 범위
- 최대값과 최소값의 차이이다.
변동성을 측정하는 가장 단순한 방법이다.
EX) 615-425=190
2. 분산
- 자료의 변동성을 측정하는 도구이다.
편차제곱의 평균을 분산이라고 한다.

+ 추가로 표본 분산의 분모 즉 자유도는 n-1이다.
그 이유는 표본평균 만으로는 정확한 뮤(모집단 평균)을
알 수 없기에 구하는 과정에서 자유도를 1 잃게 된다.
3. 표준편차
- 분산에 제곱근을 취한 값이다.
원래의 자료에서 사용된 단위와 동일한 단위로 측정되므로
분산보다 해석이 용이하다는 특징이 있다.

+ 표준편차와 평균으로 위험을 구분할 수는 없다.
값의 비교 정도만 가능하다.
4. 변동계수
- 표준편차가 평균에 비하여 얼마나 큰지를 나타낸다.

- 즉 표준편차/평균을 한 값이 변동계수가 된다.
예시)

'대학교 > 통계학개론' 카테고리의 다른 글
| 통계학개론 - (6) 이항확률분포, 포아송확률분포 (2) | 2023.03.27 |
|---|---|
| 통계학개론 - (5) 확률, 사건, 베이즈 정리 (2) | 2023.03.26 |
| 통계학개론 - (4) 수치 척도(왜도, 공분산, 상관계수) (2) | 2023.03.23 |
| 통계학개론 - (2) 기술 통계 (1) | 2023.03.22 |
| 통계학개론 - (1) 자료와 통계학 (1) | 2023.03.22 |