- 연속확률분포
연속확률변수 : 연속된 어떤 구간이나 구간들의 집합에 있는 값을 취할 수 있다.
- 특정한 값을 가진 확률변수의 확률값은 나타낼 수 없다.
대신 확률변수가 주어진 구간내에 있을 확률은 계산할 수 있다.
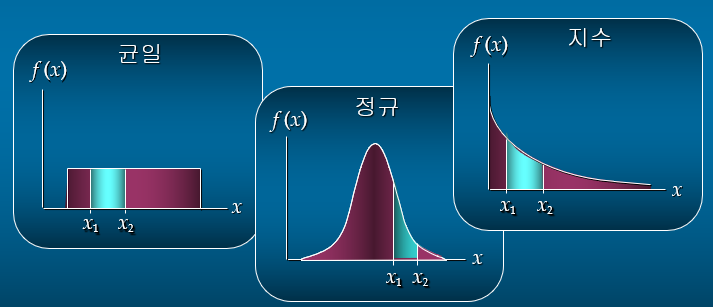
- 균일확률분포
- 확률값이 구간 길이에 비례하면 확률변수는 균일하게 분포된다.
f(x)=1/(b-a), for a<=x<=b
(b는 가장 큰 값, a는 가장 작은 값)

예시) 샐러드 무게에 대한 균일확률분포
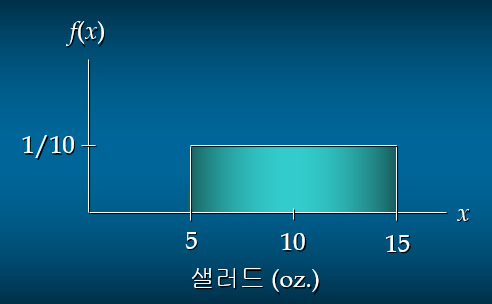
평균 : 10
분산 : 8.33
12~15온스 사이에서 가져갈 확률 : 0.3
- 정규확률분포
정규확률분포는 연속확률분포를 기술하는 가장 중요한 분포이다.

특성 : 분포의 왜도는 0이다.
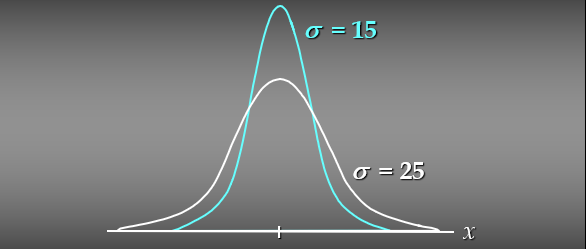
평균과 분산에 의해 정의될 수 있다.
평균에서 정규곡선이 가장 높으면, 이점이 중앙값이고 최빈값이다.
평균은 어떤 수치라도 될 수 있고, 표분편차는 곡선의 넓이를 결정한다.
+ 이항분포(n과p로 정의), 포아송분포(평균), 정규확률분포(평균,분산)
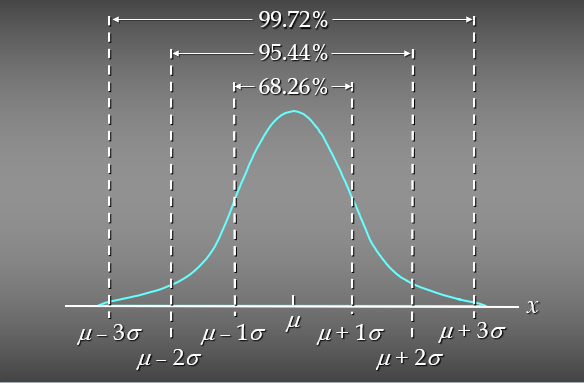
평균으로부터 +-1~3 표준편차 안에 값이 있을 확률을 나타낸 것이다.
- 표준정규확률분포
정규분포를 따르는 확률변수의 평균이 0이고, 표준편차가 1인 분포를 말한다.

z는 x가 평균으로부터 표준편차의 몇 배가 떨어져 있는 측정할 수 있다.
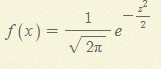
예시) 재고가 20갤런 이하로 떨어질 경우 보충 주문을 한다.
분포는 평균 15갤런과 표준편차 6갤런이다.
재고가 바닥날 확률을 얼마인가?
- z=(20-15)/6 = 0.83
- 0.83 -> 0.7967만큼 포함한다.
- 1-0.7967=0.2033% -> 바닥날 확률은 20.33%이다.
+원하는 확률로 조정하기 위해서는 z값을 이용하면 된다.
바닥날 확률을 5%미만으로 만들고 싶다면 z값이 95가 넘는
x값을 구하면 된다.
- 이항확률의 정규근사
시행횟수 n이 커지면, 이항확률함수를 계산하기 어렵다.
정규분포는 n>20, np>=5 그리고 n(1-p)>=5일 경우 근사치를 제공한다.
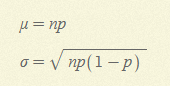
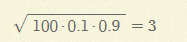
예시) 송장 100개를 표본으로 추출하였을 때 이중 12개가 오류가 있을 확률
(송장의 약 10%에서 오류를 범한다고 가정)
np=100*0.1=10
x가 12.5이하일 확률 : 0.7967
x가 11.5이하일 확률 : 0.6915
x가 12일 확률 : 0.7967-0.6915 = 0.1052
- 지수확률분포
임무완성에 걸리는 시간을 기술하는데 유용하다.
지수확률분포의 속성은 평균과 표준편차가 같다는 것이다.
지수분포는 오른쪽으로 경사진 모양이며, 왜도는 2이다.
+ 포아송분포 : 구간당 사건발생 횟수를 적절히 기술
지수분포 : 사건발생간 구간의 길이를 적절히 기술
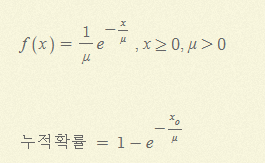
예시) 도착하는 자동차들 사이의 시간간격은 평균 3분인 지수확률 분포를 따른다.
이때 연속한 두 대의 차량이 도착하는 시간이 2분 이내일 확률은?
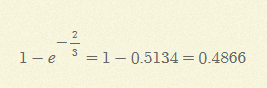
'대학교 > 통계학개론' 카테고리의 다른 글
| 통계학개론 - (9) 구간 추정 (1) | 2023.04.14 |
|---|---|
| 통계학개론 - (8) 표본추출과 점추정 (1) | 2023.04.11 |
| 통계학개론 - (6) 이항확률분포, 포아송확률분포 (2) | 2023.03.27 |
| 통계학개론 - (5) 확률, 사건, 베이즈 정리 (2) | 2023.03.26 |
| 통계학개론 - (4) 수치 척도(왜도, 공분산, 상관계수) (2) | 2023.03.23 |