반응형
- 표본추출
- 유한 모집단
규모 n인 유한한 모집단으로부터 규모 n은 표본 각각이 선택될 확률이 동일하다.
- 무한 모집단
모집단의 요소들이 계속 진행되는 과정에 있기 때문에 생성되는 요소의 수에 상한이 없다.
- 점추정
모집단 모수를 추정하기 위해 표본 통계량의 값을
계산하는데 표본 자료를 사용할 수 있다.

모집단이 정규분포일 때, 표분평균의 표본분포는 표본크기에 관계없이 정규분포이다.
대부분, 표본 규모가 30이상이면, 표본평균의 표본분포는 정규분포에 가까워진다.
모집단의 분포가 비대칭적이거나 극단값이 있는 경우, 표본 규모는 50이상이 좋다.
+ 중심극한정리
모집단으로부터 규모 n의 무작위 표본을 선택할 때,
표본평균의 표본분포는 표본규모가 커질수록 정규분포에 가까워진다.
EX) 30명의 무작위 추출 표본에 대한 평균이 1080~1100사이에서 있을 확률은?
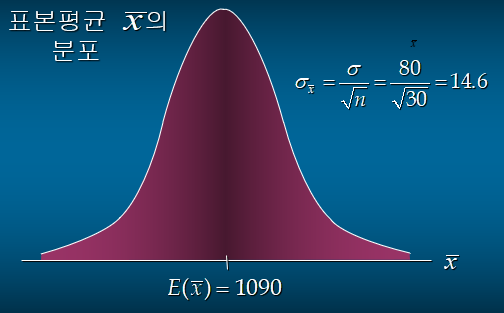
- z=(1100-1090)/14.6 = 0.68
z의 면적 = 0.7517
z=(1080-1090)/14.6=-0.68
z의 면적 = 0.2483
= 0.7517-0.2483 = 0.5034
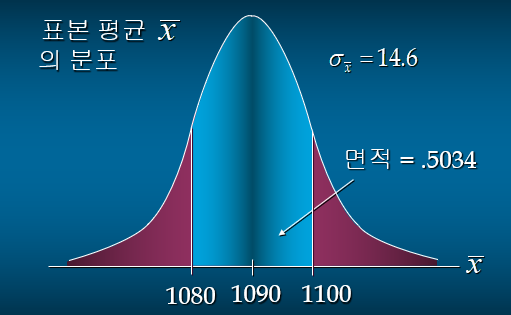
EX) 위의 30명을 100명으로 바꿀 경우
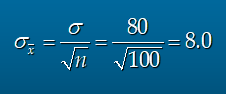
표본오차가 감소하게 된다. 즉 평균에 더 많은 값이 몰린다.
즉 1080~1100 = 0.7888이된다. 모집단 평균에 더 가까워진다.
'대학교 > 통계학개론' 카테고리의 다른 글
| 통계학개론 - (10) 가설검정 (2) | 2023.04.14 |
|---|---|
| 통계학개론 - (9) 구간 추정 (1) | 2023.04.14 |
| 통계학개론 - (7) 균일, 정규, 지수확률분포 (1) | 2023.04.01 |
| 통계학개론 - (6) 이항확률분포, 포아송확률분포 (2) | 2023.03.27 |
| 통계학개론 - (5) 확률, 사건, 베이즈 정리 (2) | 2023.03.26 |