- 두 모집단 평균 차이에 대한 추론
1. 짝 표본의 경우
짝 표본 방법에서는 추출된 각 표본항목이 한 쌍의 자료값을 가지고 있다.
EX) 두 택배사 a,b의 평균배송시간이 유의수준 0.05에서 차이가 있다고 할 수 있는가?

귀무가설 : =0, 대립가설 : !=0
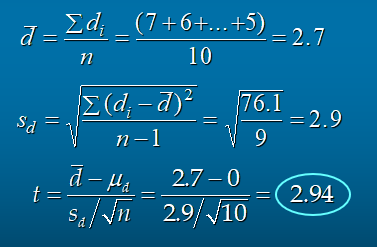
t 값은 df=9에서 2.262가 나온다. 즉 2.94>2.262이므로, 귀무가설을 기각한다.
즉 두 택배회사의 평균 배송시간에 차이가 있다는 것을 적어도 95% 신뢰한다.
2. 표준편차 2개가 알려져 있는 경우

- 신뢰구간 추정

EX) 유의수준 0.05

점추정치 : 295-278 = 17야드
구간추정 : 17+-5.14 -> 11.86~22.14 사이가 95% 신뢰
- 검정통계량

EX) 유의수준 0.01에서 Par사의 골프공의 평균 드라이빙거리가 Rap사 골프공보다 더 멀다고 할 수 있는가?
귀무가설 : 점추정치<=0
대립가설 : 점추정치 >0
검정통계량 = 6.49, z0.01 = 2.33
즉 6.49>2.33이므로 귀무가설을 기각한다.
즉 Par사 골프공이 Rap사 골프공보다 평균 드라이빙거리가 더 멀다는 것이다.
3. 표준편차 2개가 알려지지 않은 경우
- 신뢰구간 추정치
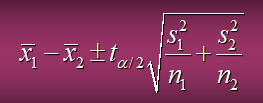
- t a/2에 대한 자유도

EX)

점추정치 : 29.8-27.3 = 2.5mpg
자유도 : 24.07
t0.05 = 1.711
구간추정 : 2.5+-1.069 -> 1.431~3.569 구간이 90% 신뢰
+ 유의수준 0.05에서 M이 J보다 mpg가 크다고 할 수 있는가?
귀무가설 : 점추정<=0
대립가설 : 점추정>0
t= 4.003
t0.05 = 1.711
4.003>1.711이므로 귀무가설을 기각한다.
즉 M의 연비가 더 우수하다는 것을 적어도 95% 신뢰한다.
'대학교 > 통계학개론' 카테고리의 다른 글
| 통계학개론 - (13) 다중회귀분석 (2) | 2023.05.26 |
|---|---|
| 통계학개론 - (12) 단순선형회귀 (3) | 2023.05.19 |
| 통계학개론 - (10) 가설검정 (2) | 2023.04.14 |
| 통계학개론 - (9) 구간 추정 (1) | 2023.04.14 |
| 통계학개론 - (8) 표본추출과 점추정 (1) | 2023.04.11 |