반응형
- 단순선형회귀
하나의 독립변수와 하나의 종속변수가 관련된다.
두 변수의 관계는 하나의 직선으로 추정된다.
두 개 또는 그 이상의 독립변수를 포함하는 회귀분석은 다중회귀분석이라 한다.
- 단순선형회귀모형

모수와 오차항으로 표기할 수 있다.
- 단순성형회귀식
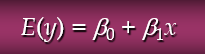
y절편과 기울기와 x값의 곱으로 y의 기대값을 표기하였다.

양의 선형관계면 회귀선이 +, 음의 선형관계면 - 0이면 기울기가 0이다.
- 추정단순선형회귀식
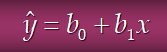
y절편과 기울기와 x값의 곱으로 y에 대한 추정값을 표현하였다.
- 최소자승법
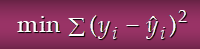
관찰값과 추정값의 차를 제곱한 것의 min을 구하는 것이다.
- 추정회귀식의 기울기와 y절편
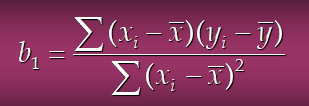
추정회귀식의 기울기는
x와y의 공분산 / x의 분산으로 구할 수 있다.
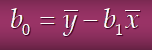
추정회귀식의 y절편은 종속변수의 평균과 독립변수의평균*기울기로 구할 수 있다.
EX) 단순선형회귀 문제

기울기
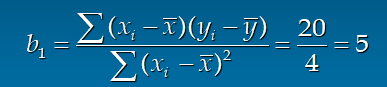
y절편
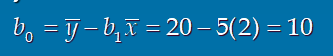
추정회귀식
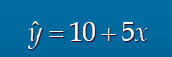
- 결정계수
SST = 총제곱합
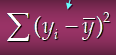
SSR = 회귀제곱합
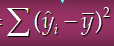
SSE = 오차제곱합
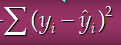
SST = SSR + SSE
- 결정계수
R^2 = SSR/SST
이 값은 회귀관계가 강한지 약한지의 여부를 알 수 있다.
- 표본 상관계수

기울기가 양수이면 양수, 음수이면 음수가 된다.
- 오차항
평균이 0인 확률변수이다.
오차항의 분산은 모든 x값에 대해 동일하다.
오차항은 서로 독립적이다.
오차항은 정규분포를 이루는 확률변수이다.
- 유의성검정
회귀관계의 유의성을 검정하기 위해서는 가설검정을 수행해야 한다.

s^2는 오차평균제곱(MSE)라고 표기한다.
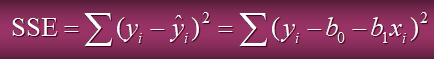
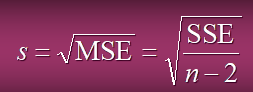
- t검정을 통한 유의성 검정


'대학교 > 통계학개론' 카테고리의 다른 글
| 통계학개론 - (14) 모집단 비율의 추정 (1) | 2023.06.10 |
|---|---|
| 통계학개론 - (13) 다중회귀분석 (2) | 2023.05.26 |
| 통계학개론 - (11) 두 집단 평균의 비교 (4) | 2023.05.05 |
| 통계학개론 - (10) 가설검정 (2) | 2023.04.14 |
| 통계학개론 - (9) 구간 추정 (1) | 2023.04.14 |