반응형
- 행렬

- 정사각행렬 : 행과 열의 크기가 같은 행렬을 말한다.

- 영행렬 : 모든 성분이 0인 행렬을 말한다.

- 행렬의 덧셈과 스칼라곱에 관한 성질
(a) (덧셈의 교환법칙) A+B=B+A
(b) (덧셈의 결합법칙) (A+B)+C = A+(B+C)
(c) (덧셈의 항등원) A+O=O+A=A
(d) (스칼라곱의 분배법칙) c(A+B)=cA+cB
- 행렬의 곱셈

A=> mXp 행렬, B=> pXn 행렬 -> AB => mXn행렬
- 행렬의 곱셈에 관한 성질
(a) (곱셈의 결합법칙) (AB)C = A(BC)
(b) (곱셈의 분배법칙) A(B+C) = AB+AC
+ AB=BA는 일반적으로 성립하지 않는다.
- 항등행렬

A X 항등행렬 = 항등행렬 X A = A
-> 실수에서의 1과 비슷한 역할을 한다.
- 전치행렬

행과 열을 바꾸는 것을 전치라고 한다.
이때 얻는 행렬을 전치행려이라 한다.

- 대칭행렬

주어진 행렬과 전치행렬이 같은 행렬을 대칭행렬이라고 한다.
- 역행렬
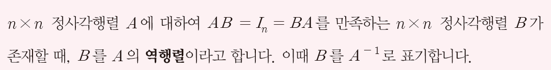
- 가역행렬 : 역행렬이 존재하는 행렬
- 비가역행렬 : 역행렬이 존재하지 않는 행렬
- 역행렬의 성질

- 2X2 행렬의 역행렬

위의 공식대로 2X2의 역행렬을 구할 수 있다.
- 행렬식
대각성분이 모두 1이고 그 외의 나머지 성분이 0인 행렬
일반적인 n X n 행렬의 역행렬의 존재 유무를 결정하는 식이다.


- nXn의 행렬의 역행렬
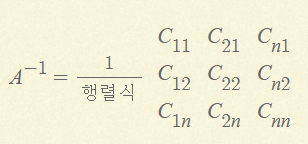
'대학교 > 인공지능수학' 카테고리의 다른 글
| 인공지능수학 - (6) 다변수 함수 (1) | 2023.05.14 |
|---|---|
| 인공지능수학 - (5) 이차형식 (2) | 2023.04.20 |
| 인공지능수학 - (4) 고윳값과 고유벡터 (2) | 2023.04.08 |
| 인공지능수학 - (3) 선형변환 (2) | 2023.03.29 |
| 인공지능수학 - (2) 선형 연립방정식, 행 사다리꼴 (3) | 2023.03.24 |