반응형
- 함수

다변수 함수 : 집합 A에 속하는 각 원소 x가 n차원의 원소인 함수이다.
정의역 : 함수 f가 정의되는 집합 A
공역 : 집합 B
치역 : 집합 A의 각 X에 대하여 함숫값 전체의 집합
- 다변수 함수의 그래프

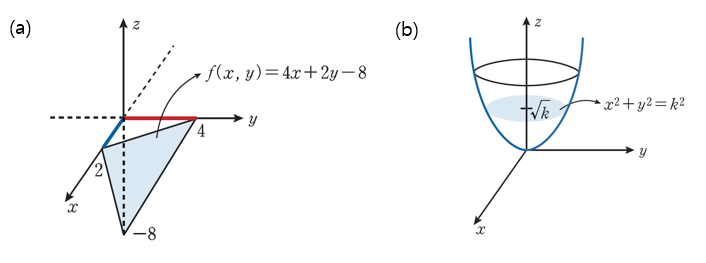
즉 절편을 찾아서 그래프를 그리면 된다.
- 레벨집합
다변수 함수의 치역에 속한 상수 k에 대하여 f(x1,~,xn)=k를 만족하는
점의 집합을 함수 f의 레벨집합이라고 한다.
등위곡선 : 함수 f가 이변수 함수인 경우, f의 레벨집합
등위곡면 : 함수 f가 삼변수 함수인 경우, f의 레벨집합


- 다변수 함수의 극한


- 다변수 함수의 극한 계산법
1. 극한이 존재하는 경우 : 모든 경로에 대하여 극한이 동일함을 보인다.
2. 극한이 존재하지 않는 경우 : 극한이 서로 다른 두 가지 경로를 찾는다.
- 다변수 함수의 연속


- 다변수 함수의 미분
- 편도함수

- 방향도함수


위 정리를 통해 쉽게 구할 수 있다.
- 미분가능한 함수
편도함수와 방향도함수를 이용해 미분가능한 함수를 정의할 수 있다.



- 다변수 함수의 연쇄법칙
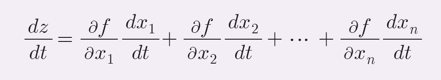

- 기울기벡터
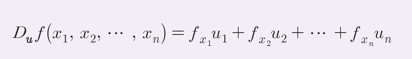
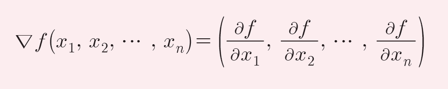
- 방향도함수와 기울기벡터
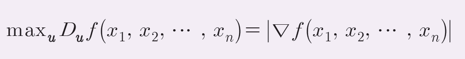
'대학교 > 인공지능수학' 카테고리의 다른 글
| 인공지능수학 - (8) 볼록함수 (2) | 2023.05.31 |
|---|---|
| 인공지능수학 - (7) 다변수 벡터함수 (2) | 2023.05.17 |
| 인공지능수학 - (5) 이차형식 (2) | 2023.04.20 |
| 인공지능수학 - (4) 고윳값과 고유벡터 (2) | 2023.04.08 |
| 인공지능수학 - (3) 선형변환 (2) | 2023.03.29 |