반응형
- 고윳값과 고유벡터


행렬 A의 고유벡터 x는 0이 아니므로 비가역행렬이어야 한다.
즉 위 식의 행렬식=0이다. 이를 A의 특성다항식이라고 한다.

고윳값과 고유벡터는 전치행렬일 때는 값을 고윳값을 가진다.
또한 A의 k승일 때도 고윳값도 k승한 값이고, 고유벡터는 그대로 x이다.
A의 역행렬의 고윳값 역시 역수한 값과 같다.
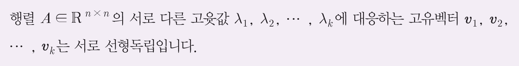
서로 다른 고윳값을 가지는 고유벡터들은 서로 선형독립이다.
즉 선형독립의 특성을 갖는다.

두 행렬이 서로 닮음관계라면, 두 행렬의 모든 고윳값은 서로 같다.
- 대각행렬
행렬 중에서 대각선을 제외한 나머지 성분들이 모두 0인 행렬을 말한다.

이는 또한 양쪽에 P를 곱하여 AP=PD도 성립한다.

동치 즉 어느 쪽을 사용하여도 같은 결과를 가져오는 것을 의미한다.

즉 행렬 A가 서로 다른 고유벡터를 가지며 선형독립이기에
이 행렬은 대각화 가능한 행렬이라는 것을 증명할 수 있다.
- 대칭행렬
정사각행렬 A와 그 행렬을 대칭한 행렬이 같은 행렬을 말한다.



여기서 직교행렬이란 P의 역행렬과 P의 전치행렬을 만족하는 가역행렬 P를 말한다.
'대학교 > 인공지능수학' 카테고리의 다른 글
| 인공지능수학 - (6) 다변수 함수 (1) | 2023.05.14 |
|---|---|
| 인공지능수학 - (5) 이차형식 (2) | 2023.04.20 |
| 인공지능수학 - (3) 선형변환 (2) | 2023.03.29 |
| 인공지능수학 - (2) 선형 연립방정식, 행 사다리꼴 (3) | 2023.03.24 |
| 인공지능수학 - (1) 행렬, 역행렬, 행렬식 (3) | 2023.03.24 |