반응형
- 이차함수
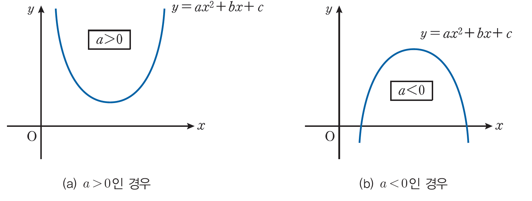
이차함수는 수학적 최적화에서 가장 기본이 된느 함수이다.
이를 통해 정부호 행렬과 정부호가 아닌 행렬을 구분할 수 있다.

만약 0보다 크거나 같은 경우는 대칭인 양의 준정부호 행렬,
0보다 작거나 같은 경우는 대칭인 음의 준정부호 행렬이라고 한다.
또한 위 네 가지 중 어느 것에도 속하지 않는 행렬을 정부호가 아닌 행렬이라 한다.
또한 대칭인 양의 정부호 행렬일 필요충분조건은 고윳값이 양수인 것이고,
대칭인 음의 정부호 행렬의 필요충분조건은 고윳값이 음수인 것이다.
- 이차형식

변수 y에 대해 x=Py로 치환하면 다음과 같이 나타낼 수 있다.
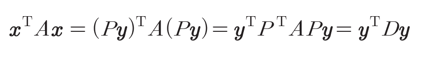
추가로 대칭인 양의 정부호 행렬이면 아래로 볼록,
대칭인 음의 정부호 행렬이면 위로 볼록,
정부호가 아닌 행렬이면 안장점을 포함한 형태이다.
'대학교 > 인공지능수학' 카테고리의 다른 글
| 인공지능수학 - (7) 다변수 벡터함수 (2) | 2023.05.17 |
|---|---|
| 인공지능수학 - (6) 다변수 함수 (1) | 2023.05.14 |
| 인공지능수학 - (4) 고윳값과 고유벡터 (2) | 2023.04.08 |
| 인공지능수학 - (3) 선형변환 (2) | 2023.03.29 |
| 인공지능수학 - (2) 선형 연립방정식, 행 사다리꼴 (3) | 2023.03.24 |