- 선형변환

- 두 조건을 모두 만족하여야 선형변환이다.
- 표준기저 : 행렬 A를 선형변환 T에 대응하는 행렬
EX) (1,0) (0,1)
- 행렬과 선형변환

- 일대일 변환과 위로의 변환

- 일대일 변환은 없거나 단 하나일 때를 말한다.
- 위로의 변환은 하나 이상, 여러 개 있을 때를 말한다.
- 선형변환과 일대일 변환

- 일대일 변환이며, 해는 유일하게 0이어야 한다.
- 닮음변환

주어진 벡터를 그 방향으로 k배 늘리는 변환이다.
- 대칭변환
x축에 대한 대칭이동 : (x,y) -> (x,-y)
y축에 대한 대칭이동 : (x,y) -> (-x,y)
원점에 대한 대칭이동 : (x,y) -> (-x,-y)
직선 y=x에 대한 대칭이동 : (x,y) -> (y,x)

- 회전변환
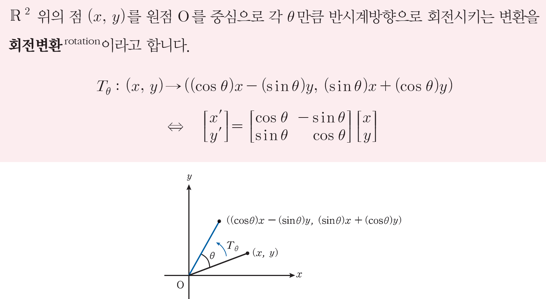
- 합성변환

합성변환을 풀이할 때 회전변환과 대칭변환으로 행렬 A,B를 구하여
합성변환에 변환되는 점을 구하는 형태도 있기에 회전변환과 대칭변환 등을 알고 있어야 한다.
- 역변환

A는 가역행렬이어야 한다.
1. 역행렬을 구한다.
2. T의 역변환 형태로 변환한다.
3. 값을 대입하여 출력한다.
- 벡터공간

10가지 조건 중 3가지 조건만으로 벡터공간의 여부를 확인할 수 있다.
이를 부분공간이라고 부른다.
- 부분공간

부분공간을 표현하는 방법 중에는 선형결과과 생성집합이 있다.
- 선형결합과 생성집합

선형독립과 선형종속. 기저를 배우기 위해선 선형결합과 생성집합의 개념을 알아야 한다.
- 선형독립

오직 0일뿐일 때만 선형독립이라고 부른다.
이외는 선형종속이라고 부른다.
이를 판별할 수 있어야 한다.
- 기저

선형독립이나 기저가 아닐 수 있다.
기저는 부분공간과 일치하기 위해, 해당 값들이 모두 있어야 한다.
- 생성집합 정리

생성집합에서 불필요한 벡터를 제거하여서 기저를 찾는 방법이다.
'대학교 > 인공지능수학' 카테고리의 다른 글
| 인공지능수학 - (6) 다변수 함수 (1) | 2023.05.14 |
|---|---|
| 인공지능수학 - (5) 이차형식 (2) | 2023.04.20 |
| 인공지능수학 - (4) 고윳값과 고유벡터 (2) | 2023.04.08 |
| 인공지능수학 - (2) 선형 연립방정식, 행 사다리꼴 (3) | 2023.03.24 |
| 인공지능수학 - (1) 행렬, 역행렬, 행렬식 (3) | 2023.03.24 |